Information & Uncertainty
One of the most surprising and interesting results of the digital age is how information is intrinsically linked to uncertainty and entropy.
Of course for this to make sense, we need to be careful about how we define what we mean by information, separating it from any subjective interpretation, so that the results are applicable to any system in which some type of message is transmitted from one point to another.
Claude Shannon, the father of Information Theory, said in the introduction to his seminal paper A Mathematical Theory of Communication:
Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem.
The problem is that in trying to place meaning or value on a particular message we must, inevitably, take the perspective of the receiver.
A message saying, “the cat is in the bag” would probably, out of context, be pretty meaningless to most people. However, suppose Alice sends this message to Bob and in advance they have agreed that this phrase is code for “The plan is going ahead. Send $10,000 by 10pm tonight”. Then in this case, there is a far greater amount of value or meaning contained within the message.
Similarly the message “Vikaar saadab oma tervitused ja palub, et sa tuled korraga” would only have intrinsic meaning for someone who speaks Estonian.
What we would like to arrive at is a method for quantifying the amount of information contained in any arbitrary message, generated by any arbitrary system, and we can get there using the tools of Information Theory. It is in this context that we begin to see the surprising relationship between information and uncertainty.
There are, in fact, two different schools of Information Theory: Classical Information Theory developed by Claude Shannon, and Algorithmic Information Theory developed by Ray Solomonoff, Andrey Kolmogorov and Gregory Chaitin.
We will look at both of these in turn.
Classical Information Theory
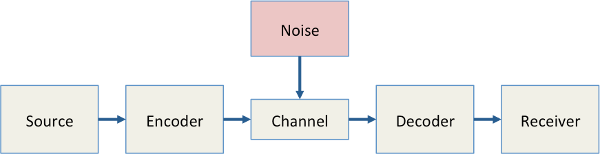
Descriptively, for any such channel
- We start with a source, for instance a piece of English text, some music or a picture
- The source is encoded according to certain rules whereby each character or element of the source is mapped to a new symbol from a well-defined set of possible symbols, called the symbol space
- We transmit the encoded message through some channel, which could be digital, visual etc., and which may be subject to interference of from a source of noise
- On the receiving end, knowledge of the symbol space is then used to decode the message back into a form recognizable to the receiver.
One of the things Shannon was interested in understanding was how many bits are needed to represent and transmit a given message.
Previously, Ralph Hartley had arrived at a measure of information:
where H is the amount of information, S is the symbol space and n is the number of symbols being transmitted.
From this equation we can see that the amount of information H, grows in line with the size of the symbol space. Why might this be?
Suppose we have a very simple system in which all we wish to communicate is a Go or Stop message. Here the Symbol Space can be thought of has having only two possibilities, say ‘1’ or ‘0’, and so in order to transmit our message we only need 1 bit of information.
Now suppose that we wish to expand our set of possible messages to have three options: Go Now, Go Tomorrow, Don’t Go, i.e. a symbol space of size 3.
In this case, 1 bit of information is no longer enough, and in fact we would need at least 1 additional bit in order to be able to reliably transmit any message, i.e.
- Go Now = 10
- Go Tomorrow = 01
- Don’t Go = 00
Here we are already beginning to see an intuitive link between the amount of information and the amount of uncertainty about the message. With a symbol space of size 2, there is a 50% chance of being able to predict the next bit, whereas with a symbol space of size 3 there are more choices and hence a lower possibility of predicting what comes next.
However this model assumes that each symbol is equally likely. What Claude Shannon did was to extend this by understanding that, in the real world, not all choices are equally likely.
For example in the English language, the letters x, y and z are far less likely to appear than the letters a, e or m. Furthermore, the next letter can actually depend on the previous letter or even the previous group or letters, so q is almost always followed by u, cl is going to be followed by a vowel etc.
Shannon arrived at a definition for what he called the entropy of a message:
where \({p}\_{i}\) is the probability of the ith bit in the message.
Shannon saw that the information content of a message is fundamentally linked to the uncertainty associated with the message. In fact we can see that entropy, and hence information content, are maximised when all probabilities are equally likely.
Perhaps an easier way to see this intuitively is through another core idea of Information Theory, that of compression.
In recognizing that the letters, groups of letters and words in the English language are not all as likely to appear, we begin to see the possibilities for compression. In fact most people are already very familiar with the idea of compression, fr nstnc by rdng th nd f ths sntnc.
The fundamental idea is that, the less random a message is, the more it can be compressed, and hence the less amount of information is needed to store and transmit it.
Take the following two sentences:
A: “word word word word word word word word word word word word”
B: “sbrgmdopbrlevgawglscjwhmoyucsaxjro peig bhzs kcttk oidomnfr”
Both are 59 characters long, however A can be compressed for transmission to “word 12 times”, i.e. only 13 characters or less than a quarter of its original length, whereas B is just a random mix of letters and so all 59 original characters would need to be transmitted.
Algorithmic Information Theory
We will go into far less detail regarding algorithmic information theory, however it is interesting to see how some very similar interpretations arise.
Whereas Shannon developed his ideas by thinking about communication channels, Algorithmic Information Theory is more concerned with the relationship between computation and information.
A core definition of Algorithmic Information theory states that ‘a binary string is said to be random if the Kolmogorov complexity of the string is at least the length of the string’1
The Kolmogorov complexity, K, shares many properties with Shannon’s entropy, S. For a given string, K is defined as being its
shortest description p on a Universal Turing machine U:sup:`2`
Fundamentally this is a measure of the amount of computing resources needed to specify the string.
More informally, we might say that given a standardized computing framework (such as a programming language), the Kolmogorov complexity is the length of the shortest program required to represent or describe the string.
Once again we return to the idea of random and non-random strings. Given the two strings:
A: “1111111111111111111111111111111111111111”
B: “0001000101011100101011101100001000010011”
Both have the same length, however A could be represented as ‘1 40 times’, whereas B has no other description than simply writing down the string itself.
Here we can see the link with Classical Information Theory. Shannon's entropy, which is a measure of information and the number of bits needed to represent a string, increases with uncertainty. Similarly, random strings are also more complex and so require more computing power or resources to represent them.
http://en.wikipedia.org/wiki/Algorithmic_information_theory#Precise_definitions http://www.hutter1.net/ait.htm