More traffic problems

Consider the following question posed on http://fivethirtyeight.com/:

There is a very long, straight highway with some number of cars (N) placed somewhere along it, randomly. The highway is only one lane, so the cars can’t pass each other. Each car is going in the same direction, and each driver has a distinct positive speed at which she prefers to travel. Each preferred speed is chosen at random. Each driver travels at her preferred speed unless she gets stuck behind a slower car, in which case she remains stuck behind the slower car. On average, how many groups of cars will eventually form? (A group is one or more cars travelling at the same speed.)

For example, if the car in the very front happens to be slowest, there will be exactly one group — everybody will eventually pile up behind the slowpoke. If the cars happen to end up in order, fastest to slowest, there will be N groups — no car ever gets stuck behind a slower car.

Overall I think it took me too long to solve, and I am sure that this isn’t the fastest way of getting to the answer, but here is my solution.

Note: It turns out that I made a silly mistake and ended up solving a slightly different problem. The mistake was due to abstracting the question too soon and only thinking about relative orders of speed in a given sequence and not taking into account that in the real world, cars will catch up with each other, and so under-counting the number of single groupings. Lesson learned.

I will leave my original solution at the bottom, because it was still an interesting problem and I ended up learning about something I didn’t know much about: Eulerian Numbers.

Correct Solution

Given a particular arrangement of the cars, we can consider a recursive algorithm for counting the number of pairings as follows:

1. Find the location of the car with the lowest velocity
2. That car and everything behind it represent 1 grouping, as all of the cars behind it have a higher speed
3. Add 1 to the number of groupings of the set of cars in front of it, etc.

This is clearly a recursive problem, where every time we add a car, the new expected number of groupings is dependent on the previous number of groupings.

To simplify the problem let us suppose, without loss of generality, that we for some n<N, we line up all of the cars in order of decreasing speed and then place them randomly on the road, starting with the fastest car and moving downward. Let’s call the number of resulting groupings G(n).

Now we add in the next slowest car, that is a car whose speed is slower than all of the existing cars on the road. There are n+1 possible positions where we can place this car, and in any location, and we can see that:

• With probability 1/(n+1) the car goes at the back and creates 1 new group, so the total number of groups is G(n) + 1
• With probability 1/(n+1) the car goes at the front and results in a total of just 1 group
• In general, with probability 1/(n+1) the new car creates 1 group consisting of all the cars behind it + the expected groupings of all the cars in front of it

and,

where \(S = \sum_{i=0}^{n-1}\mathbf{E}X_{i}+1 \Rightarrow S = n\mathbf{E}X_{n}-1\)

For N=1, we know that \(\mathbf{E}(G)=1\), so we’re done and:

which is the harmonic series.

Original Solution

The problem that my original solution answers is more like the following question:

The astronomer Simon Newcomb played the following game of solitaire. Cards numbered 1,2,....,n are shuffled, drawn and put into a pile as long as the card drawn has a number lower than its precessor. What is the average number of piles?

First of all, a couple of comments on the problem:

1. This is clearly a counting problem involving permutations: we are interested in different ways of arranging the cards, and the order matters because the relative sizes of the cards dictate the number of piles
2. In fact we can abstract away from cards and simply consider permutations of the integers 1 to N.

As mentioned in the question, the extreme cases are quite simple:

• To end up with one pile, the only possibility is having all of the integers in decreasing order of magnitude, that is to say N > N-1 > N-2 >..>2 > 1 (a strictly decreasing sequence).
• To end up with N piles, the only possibility is having all of the integers in increasing order of magnitude, that is to say 1 < 2 < 3 <… < N-1 < N (a strictly increasing sequence)

If we play around with fairly small values of N, we can see some other interesting patterns start to emerge. Let us consider, for instance, how many ways there are there of having 2 piles.

For N=3, the possibilities are:

(3,1,2), (2,1,3), (2,3,1) and (1,3,2)

For N=4, the possibilities are:

(1,4,3,2), (2,1,4,3), (2,4,3,1), (3,1,4,2), (3,2,1,4), (3,2,4,1), (3,4,2,1), (4,1,3,2), (4,2,1,3), (4,2,3,1), (4,3,1,2)

With a little bit more work, we can see that what matters is the relationship between consecutive pairs of integers, specifically whether they are < or >.

For N=4 there are three consecutive pairings, and in order to have two piles, we need two of the pairings to be > and one pairing to be <. By similar reasoning we are able to see that for general N, we need N-1 pairings to be > and one pairing to be <.

In fact, what dictates the number of end piles is the number of ascents (pairings where the 1st is < the 2^nd) or descents (pairings where the 1^st is < the 2^nd) in an ordered sequence.

Furthermore, the number of permutations of a sequence with the specific number of ascents or descents will tell us how many possible ways there are to end up with a certain number of piles.

Eulerian Numbers

It turns out that what we are looking for are numbers called Eulerian Numbers.

From Wikipedia:

the Eulerian number A(n, m), is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element (permutations with m "ascents")

It is possible to generate the Eulerian Numbers algorithmically by counting the number of permutations of N that result in a given number of groups, or alternatively using well-defined iterative or generating functions.

Again from Wikipedia, here is a table with the Eulerian Numbers for small N:

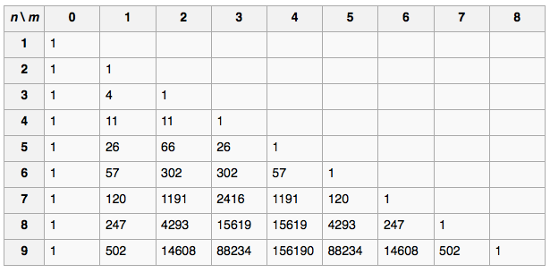
Before we get to the final solution, there are two interesting properties of Eulerian numbers that are worth noting:

• For a given row in the table above, the Eulerian Numbers for a particular N sum to N! (because we end up counting all possible permutations of N). Alternatively, we can write this as:

• There is also symmetry within the Eulerian Numbers for given n, i.e., A(n,0) = A(n,n-1), A(n,1) = A(n,n-2) etc. We can see this by repeating our arguments above for a reversed sequence of integers.

The Solution

What we are looking for is the average, or expected, number of groups (piles) for a given N.

By definition of expectation:

The probability of a given grouping is the number of ways of achieving that grouping / the total possible arrangements of N, which is given by:

Where A(N,G-1) is the Eulerian Number.

If we sum over all possible groupings, we are looking for:

We can write this sum out as follows:

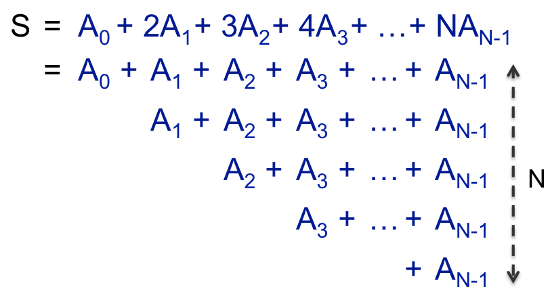
We can then fill-in the triangle in order to make a rectangle:

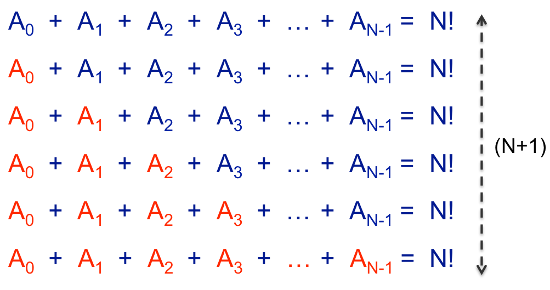
However, from the properties of the Eulerian Numbers we know that

• Each row sums to N!
• The sum of the red terms is equal to the sum of the blue terms due to the symmetry in the Eulerian Numbers.

Thus we can see that \(2S = (N+1) \times N!\), and so we get our final result:

Written by Simon Bedford in Maths on Tue 09 February 2016. Tags: maths, coding,