Some Counting Problems

I have been looking over some elementary probability recently, and spent some time thinking about a couple of questions that I think have pretty neat solutions.

1. Birthday Problem

The problem is very simply stated, but the answer is counterintuitive to most people.

What is the smallest number of people that you need in a room (or some type of gathering) for there to be a better than even chance that two people share the same birthday?

What seems to throw people off here is that they immediately try and answer a different question: What is the probability that someone else shares my birthday (or some other specific birthday)?.

In fact, we can quite quickly estimate a rough value for what this number of people should be (n). If we do not concern ourselves with a specific day, then what we are looking for is any pair of people who share the same birthday.

For some small values of n, the number of possible pairings are:

n = 18, 153 pairings (153/365 = 0.419)

n = 19, 171 pairings (171/365 = 0.468)

n = 20, 190 pairing (190/365 = 0.521)

So intuitively, we think that the answer should be somewhere around 20.

The actual calculation follows standard combinatorial reasoning:

Suppose n = 2. It turns out that it is simpler to think about the probability of the people not sharing a birthday, and then take the complement.

We can see that there are 365×365 total possible birthday combinations (365 for each person), and 365×364 combinations for them not sharing a birthday (365 possibilities for the first person, and 364 for the second as one day is now “out of the question”).

So for 2 people, the probability that they don’t share a birthday is

\begin{equation*} \frac{365 \times ~364}{365 \times ~365} \approx 0.997 \end{equation*}

For n = 3, similarly we can see that

\begin{equation*} P = \frac{365 \times ~364 \times 363}{365 \times ~365 \times ~365} \approx 0.992 \end{equation*}

In fact, for general n, by similar reasoning we can see that the probability that none of them share a birthday is:

\begin{equation*} P = \frac{365 \times ~364 \times ... \times (365-n+1))}{365 \times ~365 \times ~... \times 365} = \frac{365!}{(365-n)! \times 365^{n}} \end{equation*}

(in the numerator, each person removes a possibility for the number of allowed birthdays).

Using Stirling’s approximation, we can show that this is:

\begin{equation*} \sim e^{-n} \left (\frac{365}{365-n} ~\right)^{365-n+0.5} \end{equation*}

Once this probability drops below 0.5, then we have a better than 50-50 chance of two people sharing a birthday.

For values of n around 20, we can see that:

n = 20, P = 0.589

n = 21, P = 0.556

n = 22, P = 0.524

n = 23, P = 0.493

So we see that with only 23 people, the probability that two people share the same birthday is 0.51.

2. Boxes and balls

Suppose we have n balls that are tossed independently into n boxes. What is the probability that exactly one box is empty?

Once again let’s start by thinking about some small values of n.

If n=2, the total number of possibilities is two boxes for ball 1 x two boxes for ball 2 = 4 in total.

For one box to be empty, we only want to consider those arrangements where both balls are in one box, of which there are 2 (both in box 1 or both in box 2), so

\begin{equation*} P = \frac{2}{4} = \frac{1}{2} \end{equation*}

If n=3, suppose box 1 is empty, then we can either have two balls in box 2 and one in box 3 or one ball in box 2 and two in box 3.

So for our numerator we need three possibilities for the empty box x three ways of choosing 2 out of 3 balls x two possibilities for the box with 2 balls.

And in the denominator we have three possible boxes for each ball.

\begin{equation*} P = \frac{3 \times 3 \times 2}{3 \times 3 \times 3} = \frac{2}{3} \end{equation*}

For general n, we can use similar reasoning.

The key is seeing that with exactly one empty box, all of the remaining n-1 boxes must have exactly one ball except for one box which will have two balls.

What might this look like:

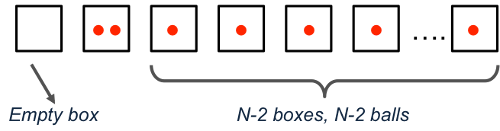
boxes-and-balls

There are n choices for the empty box. The two balls can be chosen ways. There are n-1 choices for the box with 2 balls. The remaining n-2 balls have (n-2)! arrangements among the n-2 boxes.

So the numerator is \(n \times (n-1) \times (n-2)! \times {n \choose 2}\), and the denominator is \(n^{n}\) and

\begin{equation*} \frac{n!}{n^{n}} \times {n \choose 2} = \frac{n! \times n \times (n-1)}{2n^{n}} \end{equation*}

What does this look like for small values of n?

n = 2, P = 0.5

n = 3, P = 0.667

n = 4, P = 0.563

n = 5, P = 0.384

n = 6, P = 0.231

n = 7, P = 0.129

n = 8, P = 0.067

n = 9, P = 0.0337

n = 10, P = 0.0163

In fact we can see that P reaches a maximum when n=3, and then decreases for higher values of n. This is because as the number of boxes increases, the number of possible outcomes with exactly one empty box becomes overwhelmed by all of the other possible outcomes.

Written by Simon Bedford in Maths on Tue 11 August 2015. Tags: maths,